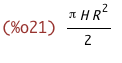/*

Um das Volumen eines Rotationskörpers auszurechnen, denken wir ihn uns waagrecht
hingelegt und betrachten nur, wie hoch er in Abhängigkeit von x aufragt. Diese Höhe
oder besser Dicke) wird beim Rotieren der Radius sein, deshalb nennen wir die Funktion
r(x).
Bei einem nicht gewölbten Sektglas der Höhe H (größter erreichbarer x-Wert) und
mit Radius R (höchster erreichbarer y-Wert) ist das eine Gerade der Steigung R/H.

(%i9) r(x,H,R):=R/H*x;

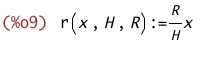
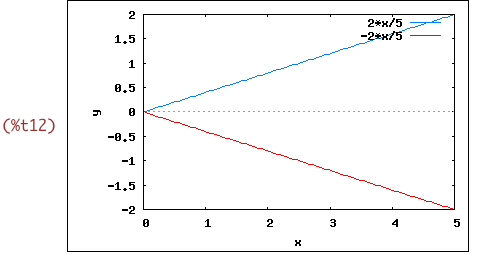
Für R=2 und H=5 sieht das Glas von der Seite so aus (der untere Teil des Graphen
wurde zusätzlich gezeichnet, damit es besser aussieht; er ist natürlich nicht
Teil der dargestellten Dickenfunktion).

(%i12) wxplot2d([r(x,5,2),-r(x,5,2)], [x,0,5], [y,-2,2])$

Das Integrieren dieser r(x)-Werte bedeutet das Aufsummieren vieler r-Stäbchen zu einer
Fläche. Das wollen wir aber nicht. Wir wollen viele Wurstscheiben zu einem Volumen
aufaddieren und brauchen deshalb die Größe der Wurstscheiben in Abhängigkeit von x.
Nennen wir es mal a(x). Mit der Kreisformel bekommen wir

(%i15) a(x,H,R):=r(x,H,R)^2*%pi;

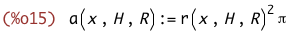
Integrieren müssen wir über die ganze Höhe. Die beginnt bei 0 und endet bei H.
Wir bekommen die bekannte Formel für das Volumen des Kegels: Das Volumen ist
genau ein Drittel des umschließenden Zylinders.

(%i16) integrate(a(x,H,R),x,0,H);

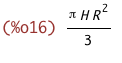
Das geht natürlich auch für schwierigere Fälle. Nehmen wir z.B. ein Sektglas in
Parabelform. Mit ein bisschen Nachdenken findet man die Dickenfunktion

(%i19) r(x,H,R):=R/sqrt(H)*sqrt(x);

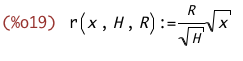
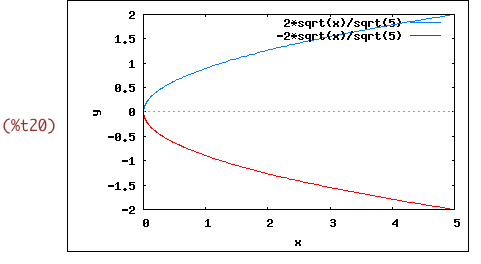
Auch dieses Glas wollen wir sehen (unterer Teile des Graphen wieder gemogelt)

(%i20) wxplot2d([r(x,5,2),-r(x,5,2)], [x,0,5], [y,-2,2])$

Das Ergebnis der Integration ist interessanterweise dem des Kegels eng verwandt.
Man sieht, dass ein parabelförmiges Glas nicht ein Drittel des umschließenden
Zylinders ausmacht, sondern die Hälfte!

(%i21) integrate(a(x,H,R),x,0,H);